Triangle problems

I have found that in large tests such as the Ohio Graduation Test, students often have trouble recognizing how to solve different problems involving right triangles. Scenarios involving right triangles are abundant in such tests, and it is vital for students to be able to approach these problems with confidence.

I am challenging my students to recognize and differentiate between the following scenarios: (1) when they know two sides of a right triangle, (2) when they know one angle and one side of a right triangle, and (3) when they know two angles. Furthermore, I am challenging them to assess what they need to find, whether it is (1) the length of a side, (2), the area of a triangle, or (3) the measurement of an angle.

I am confident that if my students become familiar with differentiating between these scenarios, they will be able to recognize when they need to use the Pythagorean Theorem, trigonometric ratios, or other geometric properties of triangles to solve a problem.

I am a teacher

As a first year teacher, I began my journey asking a lot of questions, such as "how should I best help special-ed students?", "how should I grade this assignment?", "what rules should I enforce in the classroom?" I never felt like I was the one with the answers. I was always looking to see if I was meeting expectations, and fulfilling the role I am supposed to fill.
As I have grown as a teacher, that has changed. I am now confident in my role as a teacher. I know what my students need. I know how to help them learn. I know that there is still so much that I want to learn, but I also know that I can learn it.
I am a teacher. I care. I work with passion to meet my students' needs. I give, I guide, I motivate, I provide. I am a teacher.

Exploring Pi

One of my students was frustrated by the work involved in understanding infinite series. To spark his interest, I told him that the mysterious number that he has used most of his life, pi, is actually equivalent to an infinite series.

I told him that pi is equal to the series 4 - 4/3 + 4/5 - 4/7 + 4/9 - 4/11 + ... We decided to explore this series together. We used a calculator to find 4 - 4/3 + 4/5 - 4/7 + 4/9 - 4/11. We found the this is approximately equal to 2.976. This number doesn't look very much like pi, so I suggested that we go further.

Next we used a calculator to find 4 - 4/3 + 4/5 - 4/7 + 4/9 - 4/11 + 4/13 - 4/15 + 4/17 - 4/19 + 4/21. We found that this is approximately equal to 3.232. This value is much closer to pi, and this time fell above pi, which is what we expected since we ended with a positive term.

As we continued to explore this sequence we found that the more terms we added, the closer our approximation got to pi. While this exercise didn't help the student solve problems involving geometric series, it was a small example of how fascinating math can be.

Losing a student

Last weekend, one of our students passed away in a car accident. While I didn't know her personally, it is impossible for an event like that to affect me as a teacher. As teachers, we pour so much of our lives into the lives of our students, giving ourselves to build the dreams of others. When one of those lives is snuffed out, we lose a part of ourselves.

I wish that it was possible for me to help my students always make wise choices in their lives. But that is not my role. There is no magical formula that we immediately mature my students. The process must occur naturally, through little steps at a time. I can't (and wouldn't if I could) force my students to change their habits, but I can believe in them. And when they know that I do, it can provide the seeds to the hope and courage that they need to change. And the opportunity to plant these little seeds is worth all of the sacrifices I make.

The Power to Work With Exponents

One of my students, Sarah, was really confused by the process of simplifying complicated expressions containing many different variables raised to different powers, such as: (a^2 * b^-4 * c^5)/(a * b^-2 * c^-3). I decided that the best way to help her was to give her example with numerals instead of variables, to provide the scoffolding necessary for her to understand the more abstract principles at work.

I asked Sarah to consider the multiplication of 3^2 and 3^3. If we write 3^2 as 3 * 3 and 3^3 as 3 * 3 * 3, then we can write 3^2 * 3^3 as 3 * 3 * 3 * 3 * 3. Sarah was quickly able to tell me that this can be written as 3^5, and this is why 3^2 * 3^3 is the same as 3^(2+3).

I then asked Sarah to consider 3^5/3^2. I wrote this out as (3 * 3 * 3 * 3 * 3)/(3 * 3). I asked her to simplify this expression. She canceled two of the 3's in the numerator and denominator, leaving 3 * 3 * 3. This allowed her to see why 3^5/3^2 = 3^(5-2). At this point, she was comfortable working with variables. She quickly picked up the ability to simplify expressions such as x^4/x^2. With a little more direction, she was able to conquer the more complicated expressions as well, and had a greater understanding of negative exponents as well as positive ones.

Fighting the fear of fractions

One of my students, Bonnie, was having trouble knowing how to deal with a fraction that needs to be distributed, such as 1/2(x + 10) = 20. She wasn't sure what to do with the fraction or how to solve the problem in the simplest way possible.

I encouraged her to treat the fraction like any other number. She could either distribute the fraction, or she could use division to immediately remove the fraction.

She wasn't sure how to do this at first, so I asked her to consider what she would do to "get rid of" a whole number such as 2 in an equation like 2x = 12. She suggested that she would divide both sides by two.

I suggested she apply this principle to the fraction in the first equation. If she divides both sides by 1/2, she will easily be able to solve for x. She seemed unsure of how to do this at first, so I encouraged her to explore the idea: to try it and see what happened. She canceled the halves on the left side of the equation, and then tried plugging 20 divided by 1/2 into her calculator. This enabled her to solve the problem she was working on.

A Tale of One School

In the story "A Tale of Two Cities", Miss Lucie Manette goes to France to care for her father, who has been in prison for decades. She finds him locked up in the garret of a friend; even though he is no longer in prison, he is not mentally able to cope with the reality of his freedom. Miss Manette is not able to speak to him of his freedom, because he is not prepared to understand the reality of what she says. Instead, she is forced to spark his emotions, doing her best to stir up the life that lost within him:

"If you hear in my voice--I don't know that it is so, but I hope it is--if you hear in my voice any resemblance to a voice that once was sweet music in your ears, weep for it, weep for it! If you touch, in touching my hair, anything that recalls a beloved head that lay on your breast when you were young and free, weep for it, weep for it! If, when I hint to you of a Home that is before us, where I will be true to you with all my duty and with all my faithful service, I bring back the remembrance of a Home long desolate, while your poor heart pined away, weep for it, weep for it!"

I feel like my students have been locked in their own prisons for most of their lives. My students have never been taught to explore math, to stretch their minds and think about the way the world works. Instead, they expect mathematical formulas to be spoonfed to them and hope they can remember the formulas long enough to pass tests.

Teaching my students is a process. I long to just tell them that they are free: free to explore the world and to discover math for themselves. But my students are not prepared for the freedom. When I fling the doors of their cells wide open, they stare at me like I'm crazy.

Instead, I have to stir their emotions one little step at a time. I have to ask probing questions that force them an inch outside of their cells. I have to give them glimpses of what could be, if they are will to step into the open.

It's a long journey, but I hope I'm making a little difference.

The properties of exponential functions

Robert was having trouble visualizing the graphs of exponential functions and the ways an exponential function can be generalized (the characteristics that every function of the form f(x) = a * b^x will share). I started by drawing a few diagrams for him:

Robert was able to understand that in a function f(x) = b^x, regardless of the base b, when x is 0, the function has a value of 1. This is because any base raised to an exponent of 0 is equal to 1.

I asked Robert to consider how the y-intercept would change if the function b^x times a constant a. First I gave him an example of f(x) = 2 * b^x. He told me that the y-intercept is (0, 2). I then asked him to extend this idea to any constant a. He was able to see that the y-intercept would be (0, a).

I then asked Robert to consider the range of a function f(x) = b^x. He was able to see that the function will never reach 0, or be less than 0. I then asked him to consider what would happen if he added five on the end, as in the function g(x) = b^x + 5. After the previous question, Robert quickly concluded that the range of the function is all numbers greater than 5.

Line segments unable to create a triangle

One of my students, Lucy, was having trouble understanding when it was not possible for three line segments to create a triangle. I decided the best way to help her was to give her a hands-on demonstration of why this is true, so that she could tell me why it was not possible to create a triangle with three given line segments.

I cut out three thin strips of paper. One of the strips was longer than both of the other strips combined. I asked Lucy if she could create a triangle with the three strips of paper I gave her. She was unable to do so, because the shorter strips of paper could not touch to form a third vertex when they were attached to the ends of the longer strip of paper. Lucy explained that the two strips were not long enough to make a triangle.

I created another three strips of paper. This time the long strip was the same length as both of the other strips combined. I showed her that in this case, thre three strips could make a straight line, but not a triangle.

Her face lit up as it all made sense to her. She told me, "Oh, so the two smaller lines have to be longer than the larger line!" That was what I had tried to explain to her - but it didn't make sense to her until she saw it.

Finding the missing angle in a pentagon

Last week I challenged several of my students with measurement problems from old Ohio Graduation Tests. We encoutered a problem that asked for a missing angle in a pentagon shaped like a rectangle with a corner cut out (see below. Source: Ohio Graduation Test 2004 Question 4 http://ogt.success-ode-state-oh-us.info/ItemRelease/Questions.aspx)




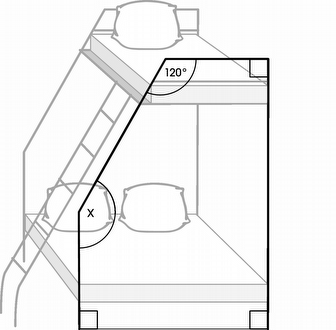
My students had no idea how to approach this problem. I suggested that the students break the shape up into triangles and rectangles, to create shapes that they are more familiar with. We broke the shape up as follows:

At this point one of my students, Sherman, was able to come up to the board and complete the problem with guidance. He broke the 120 degree angle up into two parts: the 90 degree corner and the 30 degrees left over. Sherman knew that a triangle always consists of 180 degrees, so he was able to use 180 - 30 - 90 to find the upper part of x.

Sherman thought he had his answer, but 60 degrees wasn't one of the options. I suggested that he needed to find the measurement of the whole angle x. At this point, he was able to add 60 + 90 to find the correct answer of 150 degrees.

Another approach could have been to taught students the formula for the sum of the interior angles of a pentagon. However, I knew that my students would not remember the formula or how to use it. I knew my best approach was to break the problem up into recognizable pieces.

Introduction

I teach math at a school that reaches out to dropout students. We work with a students with behavioral issues, academic challenges, and emotional instabilities.

I have found that showing students how to do advanced (or often even the most basic) mathematical procedures does not enable them to succeed at math. Something more that seeing math is required - the students have to do math, on their own.

The best way I can help my students is by asking the right questions, and letting them work through the problem on their own. This blog is about my journey in finding the right questions to allow my students to explore math for themselves.