Finding the missing angle in a pentagon

Last week I challenged several of my students with measurement problems from old Ohio Graduation Tests. We encoutered a problem that asked for a missing angle in a pentagon shaped like a rectangle with a corner cut out (see below. Source: Ohio Graduation Test 2004 Question 4 http://ogt.success-ode-state-oh-us.info/ItemRelease/Questions.aspx)




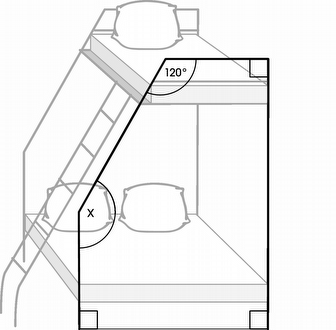
My students had no idea how to approach this problem. I suggested that the students break the shape up into triangles and rectangles, to create shapes that they are more familiar with. We broke the shape up as follows:

At this point one of my students, Sherman, was able to come up to the board and complete the problem with guidance. He broke the 120 degree angle up into two parts: the 90 degree corner and the 30 degrees left over. Sherman knew that a triangle always consists of 180 degrees, so he was able to use 180 - 30 - 90 to find the upper part of x.

Sherman thought he had his answer, but 60 degrees wasn't one of the options. I suggested that he needed to find the measurement of the whole angle x. At this point, he was able to add 60 + 90 to find the correct answer of 150 degrees.

Another approach could have been to taught students the formula for the sum of the interior angles of a pentagon. However, I knew that my students would not remember the formula or how to use it. I knew my best approach was to break the problem up into recognizable pieces.